
How to Convert Hex to Decimal
A Comprehensive Guide
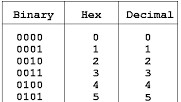
Table of Contents
How to Convert Hex to Decimal: A Comprehensive Guide
Converting hexadecimal (hex) numbers to decimal is a fundamental skill in programming and electronics. Hexadecimal is a base-16 number system used widely in computer science due to its simplicity in representing binary-coded values. This guide will walk you through the process of converting hex to decimal, provide real-world examples, and answer common questions about the conversion process. Additionally, we'll introduce you to our online tools that can help streamline this task.
Understanding Hexadecimal and Decimal Systems
Hexadecimal System
The hexadecimal system uses 16 symbols: 0-9 to represent values zero to nine and A-F (or a-f) to represent values ten to fifteen. It is particularly useful in computing as it can represent large binary numbers in a more compact and readable form.
Decimal System
The decimal system is a base-10 number system using symbols 0-9. It is the most commonly used number system for arithmetic operations in everyday life.
Step-by-Step Guide to Convert Hex to Decimal
Step 1: Write Down the Hex Number
For example, let's convert the hex number 1A3.
Step 2: Assign Powers of 16
Starting from the right, assign powers of 16 to each digit. The rightmost digit has the power 16^0, the next has 16^1, and so on:
1A3 = 1*(16^2) + A*(16^1) + 3*(16^0)
Step 3: Convert Hex Digits to Decimal
Convert each hex digit to its decimal equivalent:
1 -> 1
A -> 10
3 -> 3
Step 4: Perform the Multiplication
Multiply each digit by its corresponding power of 16:
1*(16^2) = 1*256 = 256
10*(16^1) = 10*16 = 160
3*(16^0) = 3*1 = 3
Step 5: Sum the Results
Add the results of the multiplications:
256 + 160 + 3 = 419
So, the decimal equivalent of 1A3 is 419.
Examples
Example 1: Convert 2F to Decimal
2F = 2*(16^1) + F*(16^0)
2*(16^1) = 2*16 = 32
F = 15
15*(16^0) = 15*1 = 15
32 + 15 = 47
Decimal equivalent of 2F is 47.
Example 2: Convert B4 to Decimal
B4 = B*(16^1) + 4*(16^0)
B = 11
11*(16^1) = 11*16 = 176
4*(16^0) = 4*1 = 4
176 + 4 = 180
Decimal equivalent of B4 is 180.
Common Questions
Why is Hexadecimal Used in Computing?
Hexadecimal is used in computing because it can represent large binary numbers more compactly. It simplifies the reading and writing of binary-coded values, making it easier for humans to interact with complex computer systems.
Can I Convert Large Hex Numbers to Decimal?
Yes, you can convert large hex numbers to decimal using the same process. The multiplication and summation steps may involve larger values, but the fundamental method remains the same.
Are There Tools to Automate Hex to Decimal Conversion?
Yes, there are several online tools to help automate this process. For instance, you can use our Hex to Decimal Converter for quick and accurate conversions.
Related Tools for Conversion
To assist with various conversions, explore our suite of online tools:
These tools are designed to simplify your workflow and ensure accurate results.
Conclusion
Converting hex to decimal is a straightforward process once you understand the steps involved. By breaking down the conversion into manageable parts and utilizing online tools, you can easily handle any hex-to-decimal conversion task. For a seamless and efficient conversion experience, try using our Hex to Decimal Converter and related tools available on our website.
By focusing on these steps and using the right tools, you'll master hex to decimal conversions in no time. Happy coding!
